Lo nuevo

Calculo de la distancia a una supernova con la ley de Hubble




Hoy continuamos con la historia de Terdlanbomitnbeo, sus cthulhucitos, el Palacio de Nholeghoveck y la baldosa de ytterrerrio. Si todo esto te suena a chino, ¡no leas el artículo anterior! Simplemente cierra el navegador y dedica tu tiempo a algo útil.
¿Ya se han ido? Bien, nos habíamos quedado en…
“No, mi estimado amigo”, respondió Terdlanbomitnbeo con una voz aterciopelada y viscosa, mientras fijaba casi todos sus ojos en el pequeño mamífero. “No hay ningún error”.
“No… no comprendo”, balbuceó Onaep.
“Pues debería ser bien simple, para alguien con capacidades matemáticas tan… admirables como las suyas”, susurró el monstruo. “Cada metro de oro es muy barato, sólo una milésima de Ŧ, pero ¿cuántos metros de oro hacen falta para bordear la baldosa?”
El silencio se adueñó de la sala, interrumpido únicamente por el goteo rítmico de las babas de Terdlanbomitnbeo sobre el suelo.
“Pues… pues…“
“Vamos, no es tan difícil. Hagámoslo paso a paso”, continuó el enorme Alienígena Matemático. “El borde en el paso 0, es decir, en el triángulo original de lado 1 metro, es de 3 metros”.
El pequeño Lémur asintió, algo tembloroso.
“¿Qué hay del paso 1, en el que añadimos los tres triángulos a los lados, cada uno con un tercio del lado inicial?”
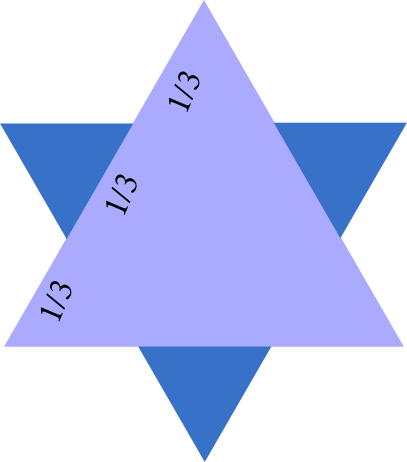
¡Calcula sub-criatura!
Onaep, bastante nervioso, pensó durante unos momentos. “Bien, cada segmento del borde tiene 1/3 metros, y hay 12 segmentos, de modo que el borde de la baldosa sería ahora de 12/3 = 4 metros.”

El Alienígena asintió, complacido, mientras sus tentáculos eran recorridos por un leve temblor de placer. “Efectivamente, sub-criatura. Pero ¿qué hay del siguiente paso, el paso 2? ¿Cuál es la longitud del borde de la baldosa entonces?”
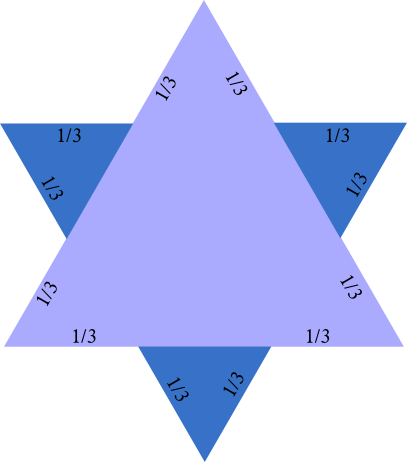
¡Calcula, sub-criatura!
“Bueno, eso tampoco es tan difícil”, respondió Onaep, algo más animado. “Cada segmento del borde mide la tercera parte que antes, es decir, 1/9 metros. Y hay… veamos…“, y el Lémur se puso a contar con el dedo, segmento a segmento, todos los tramos del borde de la baldosa, ante la mirada impaciente y despectiva de Terdlanbomitnbeo. “Hay 48 segmentos, luego la longitud del borde es ahora 48/9, unos 5,33 metros.”
“Impresionante”, sonrió el malévolo Terdlanbomitnbeo con un sarcasmo corrosivo. “Creo que no tendrá usted un problema en decirme cuál será la longitud en el paso… bueno, en el paso genérico n”.
“No puede ser muy difícil, no… sólo tengo que ver cómo varía la longitud en cada paso, y… hmm…
¡Calcula, sub-criatura!
“En cada paso hay cuatro veces más tramos que en el anterior”, razonó el Lémur. “Pero cada tramo mide la tercera parte que en el anterior paso. De manera que la longitud en cada paso es 4/3 que en el paso anterior. Como la longitud en el paso cero era 3 metros, ¡la longitud en el paso n será 3·(4/3)n!”
Splosh, splosh, splosh… Varios tentáculos de Terdlanbomitnbeo aplaudieron viscosamente ante el resultado del Lémur. “Excelente”, anunció con voz gorgoteante. “Pero entonces, tras infinitos pasos, la longitud total es…“
La carita de Onaep palideció mientras sus ojos se abrían desorbitados. Mientras, el cuerpo entero de Terdlanbomitnbeo se estremecía con oleadas de placer obsceno ante el sufrimiento de la pequeña criatura.
“Sí, sí, incluso usted lo comprende ahora…“, anunció el monstruo, abandonando ya cualquier resquicio de cortesía. “¡4/3 es mayor que 1! Por lo tanto, al hacer n infinito, la longitud del borde de la baldosa se hace… infinita, por supuesto. Independientemente del precio del metro de oro, me temo que nos debe usted una cantidad… considerable.”
El Lémur tragó saliva.
“Pe, pe, pero… ¿no hay alguna otra manera de arreglar esto?”, balbuceó con una vocecilla apenas audible.
“Por supuesto que la hay”, respondió Terdlanbomitnbeo mientras su sonrisa se abría hasta que los extremos casi se tocaban en su nuca, mostrando filas y filas de dientes amarillentos y rezumantes de babas. El olor a amoníaco se hizo insoportable, y los ojitos del pequeño Lémur se llenaron de lágrimas, en parte al menos, a causa del amoníaco.
Y es que Onaep nunca cometía errores de cálculo, y prácticamente nunca olvidaba ningún detalle. Prácticamente.
En cualquier caso, así fue como todas las propiedades del Sátrapa de Aquila fueron a parar al malvado Terdlanbomitnbeo (que las vendió rápidamente al Imperio, por supuesto); y el secretario Onaep –a petición del propio Sátrapa– fue a parar al tercer estómago del monstruo. Poco imaginaban los habitantes de Nholeghoveck lo que les esperaba entonces, pero eso es otra historia, y tendrá que esperar a otra ocasión.
Bien, pacientísimo lector: si has seguido las dos partes del artículo hasta ahora, has construido tú mismo un fractal; a diferencia de la línea que hicimos cuando presentamos a los cthulhucitos, esta vez es un fractal con todas las de la ley: el denominado copo de nieve de Koch. Antes de seguir hablando de él, un par de imágenes para disfrutar de su belleza:
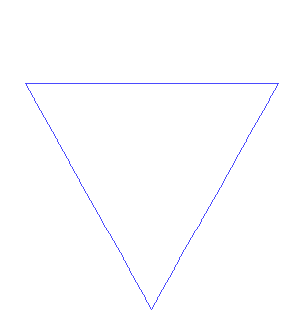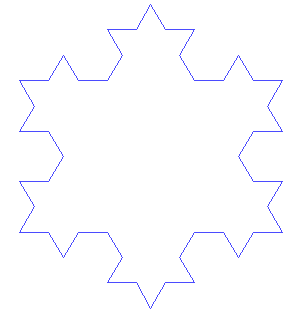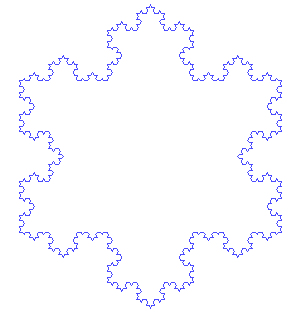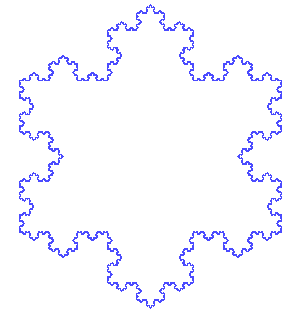
Aunque creo que si has llegado hasta aquí comprendes “hasta dónde llega” la complejidad del copo (es decir, hasta el infinito), tal vez esta animación, en la que se simula hacer “zoom” sobre uno de los lados hasta el infinito, te ayude a asimilarlo. A Onaep le hubiera sido muy útil.
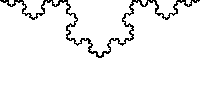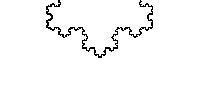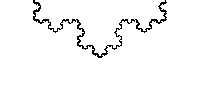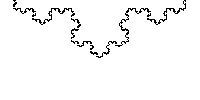
Simulación de un “zoom” en un lado del copo de nieve (dominio público).
Esta figura fue uno de los primeros fractales propuestos. Lo hizo el matemático sueco Helge von Koch en un artículo titulado “Sobre una curva continua sin tangentes construible a partir de geometría elemental” y publicado en 1904. Lo que me parece maravilloso sobre su copo de nieve es precisamente lo sencillo de su definición y lo simple de su construcción, cuando lo que se obtiene es una curva fractal.
Pero mucho más ilustrativo que mis palabras, y más impresionante que la animación anterior, es este vídeo:
¿Qué quiere decir que esta figura es un fractal, mientras que nuestra curva de los cthulhucitos del artículo de hacer tiempo no lo fue? La clave de la cuestión es la dimensión de la curva. Todos entendemos el concepto “normal y corriente” de dimensión, denominada dimensión topológica: la de una línea es 1, la de una superficie es 2, la de un volumen es 3.
Sin embargo, ese concepto de geometría euclidiana no es muy útil cuando se tienen curvas como el borde de nuestra baldosa: aunque la baldosa tiene una superficie finita, su borde es infinito. Además, aunque el borde es continuo (es decir, no hay huecos, sino que es un borde que delimita completamente la baldosa), en ningún punto es una curva “suave”.
Más técnicamente –esto te ayudará especialmente si sabes algo de cálculo infinitesimal–, el borde de la baldosa es continuo en todas partes, pero no es derivable en ninguna parte. Es imposible dibujar una tangente al borde, porque todo el borde es “pico”. Esto le pasaba también a nuestra curva de la paradoja de los cthulhucitos, por cierto.
Dicho con otras palabras: ¿en qué puntos del borde de la baldosa no hay una “esquina”? ¡En ninguno! Da igual qué punto elijas, si haces el proceso infinitas veces, en ese punto va a haber una esquina. Es como si la curva estuviera quebrada en todas partes, y de hecho por eso tiene una longitud infinita sin ocupar un espacio infinito en el suelo. Digo esto para poner de manifiesto que no es una curva “normal” para la que la dimensión topológica de toda la vida sea muy útil: es una curva “rara”.
Piensa que, en el caso de una curva normal, nos basta un número para indicar dónde estamos. Por ejemplo, el borde del triángulo inicial de la historia tiene una longitud de 3. Si tomamos como origen un punto cualquiera del triángulo, podemos determinar dónde nos encontramos sobre cualquier punto del borde con un número – 1, 2, 2.24, lo que fuese.
Incluso en el caso de curvas más raras que las de ese triángulo inicial, como nuestra curva de los cthulhucitos en “escalera” entre dos ciudades, podemos hacer lo mismo: con un número sabríamos a qué distancia estamos de cualquiera de las dos ciudades, puesto que la línea que definimos, aunque estaba quebrada en todas partes, tenía una longitud finita. Y ésa es la diferencia fundamental entre ambas: nuestra curva de la paradoja de los cthulhucitos era continua en todas partes, tenía esquinas en todos los puntos –no era derivable en ninguno–, pero al tener longitud finita, era al menos asequible en cuanto a su dimensión.
Pero ¿qué hay del borde de la baldosa? ¿Podemos saber en qué punto estamos con un número? ¡No! Tiene una longitud infinita, con lo que no vale dar un número para saber dónde estamos… su dimensión topológica es 1, pero no se comporta como una curva de dimensión 1. Es “rara” en un sentido en el que ni siquiera nuestra línea anterior de los cthulhucitos lo era.
Es común, para describir este “grado de rareza” definir una dimensión fractal. La manera más común de hacerlo es la siguiente, que voy a describir primero para algo que no sea fractal, de modo que veas cómo funciona en un caso más asequible a mentes que no son de Alienígenas Matemáticos, y luego pasamos a fractales.
Si tenemos una figura en dos dimensiones normal y corriente, como un cuadrado, podemos partir el cuadrado en trozos similares a él, por ejemplo, así:

Hemos construido una figura autosimilar, es decir, cada cuadrado pequeño es idéntico al grande pero más pequeño. Podemos ahora calcular dos cosas diferentes:
La respuesta a la primera pregunta es que cada cuadradito tiene 1/2 del lado del cuadrado anterior, es decir, es 2 veces más pequeño. Si volviéramos a dividir cada cuadradito en otros del mismo modo, tendríamos que cada uno tiene un lado 1/2 del lado del cuadrado del que partimos antes.
La respuesta a la segunda pregunta es que hay 4 cuadraditos más que antes (había uno, ahora hay cuatro). Si dividiéramos cada cuadradito del mismo modo, tendríamos 16 cuadraditos en vez de 4.
De hecho, podríamos hacer este proceso infinitas veces: siempre obtendríamos cuatro veces más cuadraditos de lado la mitad que en el paso anterior. Al cabo de n pasos, tendríamos 4n cuadraditos de lado 2n veces menor. La dimensión fractal de una figura autosimilar suele definirse comparando estos dos valores: el número de piezas autosimilares que surgen y el tamaño de cada pieza, del siguiente modo:
d=logNlogD
d=logNlogD
Donde N es el número de piezas que habrá en el paso n, y D es la disminución de tamaño del lado de cada pieza comparada con la original.
En el caso del cuadrado, su dimensión topológica de toda la vida es 2. Pero ¿cuál es su dimensión fractal? En el paso n hay 4n cuadraditos de lado 2n veces menor que el inicial, con lo que N = 4n y D = 2n:
d=log4nlog2n=log4log2=2
d=log4nlog2n=log4log2=2
Su dimensión fractal es 2, la misma que la topológica… porque el cuadrado no es un fractal, es una figura normal y corriente. De hecho, un fractal es precisamente eso: es una figura cuya dimensión fractal no coincide con su dimensión topológica. Y el nombre se debe al hecho de que se trata siempre de una dimensión que no es entera.
Básicamente, lo que hemos hecho aquí es relacionar el espacio que ocupa algo con el grado de zoom que aplicamos. En una línea “normal” de dimensión 1, por ejemplo, si aumentas el zoom al doble, ves el doble de línea, si aumentas 10 veces, ves 10 veces más línea: la dimensión es 1, que es la misma que la dimensión topológica de toda la vida.
En un plano como el cuadrado de la figura de arriba, cuando haces zoom al doble, ves cuatro veces más superficie, si aumentas el tamaño 10 veces ves 100 veces más superficie, etc. La dimensión es 2, es decir, una vez más, la dimensión topológica. Tanto la línea como la superficie –como un cubo, si lo hiciéramos con él– “ocupan lo que deben”.
Pero veamos qué sucede con el borde de nuestra baldosa. Hemos visto ya que el lado de los triangulitos es siempre la tercera parte que en el anterior, de modo que en el paso n el lado de cada triangulito era 3n veces menor que el triángulo original. Por lo tanto, para nuestra baldosa –es decir, para el copo de nieve de Koch–, D = 3n.
Por otro lado, en cada paso había 4 veces más triangulitos que en el anterior, luego en el paso n habrá 4n triangulitos. Así que para nuestra baldosa N = 4n. ¿Cuál es su dimensión fractal entonces?
d=log4nlog3n=nlog4nlog3=1,261859…
d=log4nlog3n=nlog4nlog3=1,261859…
La dimensión topológica del borde de la baldosa, dado que es una línea, es 1, pero su dimensión fractal es 1,26, luego el borde de nuestra baldosa es un fractal: no es una línea normal, pero tampoco es, como el cuadrado, una superficie. Es como si fuera una línea que ocupa más de lo que debería ocupar una línea, luego su dimensión está entre 1 y 2.
Puedes mirarlo así: si el borde de la baldosa fuera una línea de dimensión 1, al aumentar el tamaño al doble veríamos el doble de figuras autosimilares. Sin embargo, a lo largo del artículo anterior fuimos aumentando el “zoom” tres veces en cada paso, pero en vez de aparecer tres veces más figuras idénticas, como hubiera sucedido en una curva normal, veíamos cuatro veces más.
No es una superficie, pues no había nueve veces más, pero no es una línea al uso, pues no hay tres veces más. Por tanto, no tiene dimensión 1 como una línea, pero tampoco tiene dimensión 2 como una superficie. Ocupa más que una línea, pero no ocupa tanto como una superficie.
Sí, sí, ya lo sé: es muy raro, y no he llegado siquiera a rozar con los dedos la complejidad que tiene. Pero este artículo pretende ser una simple introducción, de modo que, si quieres aprender más sobre fractales, te recomiendo que leas textos más elevados; seguro que algún lector tiene sugerencias al respecto. Eso sí, nunca olvides esto aunque aprendas mucho sobre fractales de gente que sabe infinitamente más que yo: construiste tu primer fractal aquí, y fue una baldosa.
Por mi parte, simplemente te recomiendo que, si vas a encargar baldosas, dejes bien clara una cosa con la empresa a quien contrates: “Disculpe, pero la dimensión fractal del borde de las baldosas que va a ponerme coincide con su dimensión topológica, ¿verdad?” Si le dices eso, nada puede ir mal.
Para saber más (esp/ing):
Créditos: Pedro Gómez-Esteban González. (2009). El Tamiz. Recuperado de: https://eltamiz.com/